The DSP Survival Guide: What You Really Need to Know for the Midterm

Disclaimer: this is an AI-generated article intended to highlight interesting concepts / methods / tools used within the Foundations of Digital Signal Processing course. This is for educating students as well as general readers interested in the course. The article may contain errors.

Impulse responses, z-transforms, frequency filters, and the strange power of convolution—this is your no-fluff roadmap to mastering the first half of your digital signal processing course.

If you’re in the middle of a graduate-level digital signal processing course, congratulations: you’re officially in deep. By now, you’ve wrestled with delta functions, decoded difference equations, squinted at z-plane plots, and maybe even cursed at a phase response graph that made no intuitive sense.

Your exam is coming. You’re reviewing the notes. It’s overwhelming. So here’s a better idea: let’s walk through the big ideas, the ones that actually matter—and not just because they’re on the test. These are the concepts that form the backbone of digital signal processing, and understanding them doesn’t just help you pass a midterm. It gives you tools to analyze the world.

🧱 Signals and Systems: The Ground You Walk On

Signals

A signal is a function that conveys information—could be voltage over time, pressure in air, pixel intensity, or stock prices. In DSP, we care about discrete-time signals: sequences of numbers $x[n]$ , usually sampled from a continuous-time signal $x(t)$ .

Systems

A system is anything that takes a signal as input and spits out another signal. Think of it as a signal processor. The key properties you should know:

Linearity: If $x_1[n] \rightarrow y_1[n]$ and $x_2[n] \rightarrow y_2[n]$ , then $a x_1[n] + b x_2[n] \rightarrow a y_1[n] + b y_2[n]$
Time invariance: If a delay in input causes the same delay in output.
Causality: Output at time 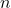$n$ depends only on current and past inputs.
Stability: A bounded input gives a bounded output (BIBO).

These properties guide everything from filter design to implementation. They’re not just theoretical—they’re practical sanity checks.

🚀 Impulse Response and Convolution: Your System’s DNA

If you understand just one thing before your exam, let it be this:

A linear time-invariant (LTI) system is completely characterized by its impulse response $h[n]$ .

Give the system a discrete-time delta function $\delta[n]$ , and the output is $h[n]$ . Any other input can be expressed as a sum of scaled and shifted deltas, so the output becomes a convolution: $y[n] = x[n] * h[n] = \sum_{k=-\infty}^{\infty} x[k] h[n-k]$

Master this. It’s how filters work. It’s how you move between time and frequency domains. It’s the essence of DSP.

📏 Inner Products and Orthogonality: Measuring Signals

You’ve seen inner products in your linear algebra class. Here, they show up as a way to measure similarity between signals: $\langle x, y \rangle = \sum_{n=-\infty}^{\infty} x[n] y^*[n]$

Where $y^*[n]$ is the complex conjugate of $y[n]$ . If the inner product is zero, the signals are orthogonal—they don’t “interfere” with each other. Orthogonality is a major theme when we get to Fourier analysis.

🧮 Difference Equations: The Backbone of Discrete-Time Systems

Many real-world DSP systems are described by linear constant-coefficient difference equations (LCCDEs): $y[n] - a_1 y[n-1] - \dots - a_N y[n-N] = b_0 x[n] + \dots + b_M x[n-M]$

Solving these involves either:

Time-domain recursion, or
Taking the z-transform, turning it into algebra.

🔁 The z-Transform: Algebra for Time-Domain Engineers

The z-transform is your bridge from messy time-domain sums to neat algebraic expressions: $X(z) = \sum_{n=-\infty}^{\infty} x[n] z^{-n}$

The power? It converts convolutions into multiplication: $x[n] * h[n] \xrightarrow{\mathcal{Z}} X(z) H(z)$

You’ll be asked to:

Take z-transforms
Invert them (using partial fractions or long division)
Analyze poles and zeros (the roots of the numerator and denominator)
Understand Region of Convergence (ROC)

And remember: the system is causal and stable if:

ROC is outside the outermost pole,
And includes the unit circle $|z| = 1$ .

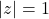📉 Poles, Zeros, and System Behavior

Poles (values of $z$ where the system blows up) determine stability and resonance.
Zeros are where the system cancels certain frequencies.

Plot them on the z-plane. You’ll often be asked to sketch frequency response based on their positions. Poles near the unit circle? Expect peaky behavior.

🎵 The Fourier Transforms: Seeing in Frequency

CTFT and DTFT

Continuous-Time Fourier Transform (CTFT): $X(f) = \int_{-\infty}^{\infty} x(t) e^{-j 2 \pi f t} dt$
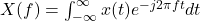
Discrete-Time Fourier Transform (DTFT): $X(e^{j\omega}) = \sum_{n=-\infty}^{\infty} x[n] e^{-j\omega n}$

These transforms show how much of each frequency exists in a signal. The DTFT is periodic with period $2\pi$ , and it’s defined for aperiodic sequences.

⚙️ Magnitude and Phase Response

Every frequency response $H(e^{j\omega})$ can be expressed as: $H(e^{j\omega}) = |H(e^{j\omega})| e^{j\angle H(e^{j\omega})}$

The magnitude tells you how much a frequency is amplified or attenuated.
The phase tells you how much a frequency component is delayed or shifted.

Don’t ignore phase—it shapes how real signals behave, especially when time alignment matters.

🎚️ Frequency-Selective Filters

Filters that target certain frequency bands:

Low-pass: keep low frequencies
High-pass: keep high frequencies
Band-pass: let a narrow band through
Band-stop: reject a narrow band

These are implemented via convolution or via IIR/FIR structures derived from poles and zeros.

🕳 Filter Properties

When analyzing filters, you care about:

Causality: Is it implementable in real time?
Stability: Does it explode with bounded input?
Linear phase: Important in audio/image to preserve waveform shape
Group delay: Related to phase slope—flat group delay avoids distortion

⏱ Sampling and Reconstruction

This is where CT and DT worlds meet. To sample a continuous signal:

Use ideal sampling: $x[n] = x(nT)$
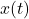If $x(t)$ is bandlimited to 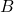$B$ , sample at 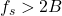$f_s > 2B$ (Nyquist rate)

Aliasing occurs if you sample too slowly—frequencies get folded over. Once that happens, you can’t recover the original signal.

Reconstruction (in theory) uses an ideal sinc interpolator: $x(t) = \sum_{n=-\infty}^{\infty} x[n] \cdot \text{sinc}\left( \frac{t - nT}{T} \right)$

In practice? Approximate it with good-enough filters.

🧊 Discrete Fourier Transform (DFT)

The DFT takes a finite-length signal and expresses it as a sum of discrete frequencies: $X[k] = \sum_{n=0}^{N-1} x[n] e^{-j 2\pi kn/N}$

Fast to compute (FFT algorithm).
Interpreted as samples of DTFT.
Circular convolution replaces linear convolution—watch out on exams!

💡 Tips to Master These Topics

Don’t memorize—understand. Why does convolution work? What does a pole at 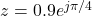$z = 0.9e^{j\pi/4}$ mean? Dig into the intuition.
Sketch things. Especially for poles/zeros, frequency responses, impulse responses.
Know your transforms. Be fluent with z-transforms, inverse z, and DFT expressions.
Be able to explain stability and causality in words. Often tested conceptually.
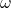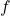Watch units and domains. Is this CTFT or DTFT? Are we talking $z$ , $\omega$ , or $f$ ? Clarity matters.

🧠 Final Thought: DSP Isn’t Just Math—It’s Structure

If you zoom out, this whole first half of the course is about one thing: structure.

How is information structured in time? In frequency? How do systems change that structure? How do we design systems that shape signals the way we want?

Master these foundations, and the next steps—filter design, adaptive systems, spectral analysis, and modern AI applications—will feel less like magic and more like engineering.

Good luck on your exam—and remember: convolution may be annoying to compute, but it’s one of the most powerful ideas in the signal universe.

Signal Processing

The DSP Survival Guide: What You Really Need to Know for the Midterm