The Hidden Framework Behind Your Favorite Tech: Why Linear Time-Invariant Systems Still Rule the World

Disclaimer: this is an AI-generated article intended to highlight interesting concepts / methods / tools used within the Foundations of Digital Signal Processing course. This is for educating students as well as general readers interested in the course. The article may contain errors.

From Spotify equalizers to climate models, one deceptively simple idea shapes modern life—whether or not you ever took a signals course

There’s a secret lurking beneath your noise-canceling headphones, your AI-powered photo filter, and even some of the tools used to predict stock markets and brain activity. It’s not AI. It’s not quantum computing. It’s something far older—and, in its way, far more elegant.

We’re talking about linear, time-invariant systems—or LTIs, if you’ve seen them scrawled across lecture boards in engineering classes. If that phrase makes your eyes glaze over, you’re not alone. But here’s the twist: understanding LTIs doesn’t just help electrical engineers or control theorists. It gives you a mental model for how inputs become outputs—in machines, in math, even in thought.

This article is a case for why students—and really, anyone interested in how the modern world works—should give LTIs the credit (and curiosity) they deserve.

🎛️ What Is a Linear Time-Invariant System?

An LTI system is a machine (physical or abstract) that processes input signals according to two simple rules:

Linearity: If you double the input, you double the output. If you add two inputs, their outputs add. Mathematically: $S[a x_1(t) + b x_2(t)] = a S[x_1(t)] + b S[x_2(t)]$
Time-invariance: If you shift the input in time, the output shifts by the same amount. The system doesn’t “care” when the signal shows up—it behaves the same today as it did yesterday.

These sound boring, right? Almost restrictive. But here’s the twist: they unlock mathematical superpowers.

🔍 Why Engineers (and Scientists, and Data Nerds) Love LTI Systems

Thanks to their simplicity, LTIs are predictable, analyzable, and stable under a wide range of conditions. Some useful implications:

Impulse response: The entire behavior of an LTI system is captured by how it responds to a single pulse. Once you know that, you can compute the output for any input by convolution: $y(t) = x(t) * h(t) = \int_{-\infty}^\infty x(\tau) h(t - \tau) d\tau$
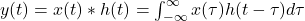
Fourier and Laplace transforms: These tools make it easy to move between the time domain and frequency domain. Filtering becomes multiplication. Differential equations become algebra.
Stability and causality: These properties can be analyzed systematically. Want a system that doesn’t explode over time? Want it to only depend on past (not future) inputs? LTI theory has checklists for that.

🧠 From Theory to Practice: Where LTI Systems Show Up

Now let’s stretch out of electrical engineering and into the messy, beautiful, interdisciplinary world where LTI ideas quietly run the show.

1. Audio & Media Tech

Noise-canceling headphones apply inverse filters to incoming sound—an LTI system trained to subtract specific frequencies.
Reverberation models in music production simulate echoes using convolution with impulse responses of concert halls.

And yes, your Spotify equalizer? It’s just a bank of finite impulse response filters—a classic LTI structure.

2. Control Systems and Robotics

Autonomous vehicles? Drones? Smart thermostats?

LTI models form the foundation of PID controllers, state-space modeling, and feedback loop design. They’re not perfect, but they offer low-complexity, high-trust approximations that still dominate industrial control systems. And in early AI–robotics integration, interpretable LTI blocks often coexist with black-box neural networks for safety and reliability.

3. Data Science and Time Series Analysis

The heart of time series modeling? You guessed it: linear filters.

ARMA and ARIMA models are linear systems applied to past values and noise.
Signal smoothing or trend detection often uses moving averages or exponential filters—textbook LTI behavior.

Even in finance, where chaos reigns, traders still deploy Kalman filters, an LTI-based estimator with recursive prediction and update steps.

4. Neuroscience and Brain Interfaces

Ever seen EEG brainwaves? That data is processed through bandpass filters to isolate alpha, beta, and gamma waves—standard LTI filtering.

Researchers also use impulse response functions to model how the brain responds to stimuli—akin to an LTI system driven by external “pulses” like light, sound, or even thought.

5. Machine Learning (Surprise!)

While modern machine learning may look nonlinear and mysterious, some of its structure borrows heavily from LTI intuition:

Convolutional Neural Networks (CNNs) apply filters over space—originally inspired by linear time-invariant filtering in signal processing.
Attention mechanisms sometimes resemble adaptive filters: weighted sums of past inputs, reminiscent of convolutional systems.

Even in transformers, once you squint past the jargon, you’ll find sliding inner products, kernel functions, and linear mixing—familiar territory to anyone who’s studied LTI systems.

📏 When Linear Models Aren’t Enough—But Still Useful

Of course, not everything is LTI. The world is nonlinear, time-variant, and full of chaos. But here’s the thing:

Linear models are often the best place to start—and the best way to debug.

Whether it’s modeling a climate system, designing a biomedical sensor, or building a voice assistant, LTI systems offer:

Interpretability: You know what the system is doing and why.
Computational efficiency: Many LTI operations are convolution-based, and convolution is fast.
Robustness: They behave consistently, which helps in safety-critical systems.

Even nonlinear control strategies often linearize their models around setpoints using—you guessed it—LTI approximations.

🧰 Skills That Pay Off

If you’re a student wondering where to focus your energy, here’s what understanding LTIs gets you:

Convolution math (great for DSP, ML, physics)
Frequency domain analysis (great for any system involving waves or periodicity)
Transfer functions and impulse response intuition
A foundation for state-space models, filter design, and even system identification

And if you’re thinking about jobs in AI safety, robotics, biomedical devices, climate modeling, or digital content creation—guess what? LTI concepts are quietly running under the hood.

🎬 Final Thought: The System That Keeps on Giving

Linear, time-invariant systems aren’t sexy. They’re not hyped. But they’re timeless (ironically). They give us a language for understanding systems that are simple, stable, and stunningly powerful. They remind us that even in the most chaotic world, there’s often a core of elegant structure waiting to be uncovered.

So next time you hear the words “impulse response” or “filter,” don’t tune out. You might be on the edge of discovering the most useful math model you’ll ever meet.

And the best part? Once you know the rules of LTIs, the rest of the world starts making a lot more sense.

audio engineering data science Signal Processing

The Hidden Framework Behind Your Favorite Tech: Why Linear Time-Invariant Systems Still Rule the World