The Inner Product: The Most Important Math You’re Already Using Without Realizing It

Disclaimer: this is an AI-generated article intended to highlight interesting concepts / methods / tools used within the Foundations of Digital Signal Processing course. This is for educating students as well as general readers interested in the course. The article may contain errors.

From Netflix recommendations to noise cancellation to neural networks—how one elegant idea powers the world of signals, learning, and beyond

If you’ve ever used Spotify, trained a neural network, filtered an image, or Googled anything—you’ve relied on an idea so fundamental it barely gets named in everyday conversation: the inner product.

It’s not flashy. It’s not mysterious. It’s certainly not trending on TikTok. But the inner product—also known as the dot product—is quietly powering the smartest algorithms and signal tools in existence. It’s the mathematical handshake that lets one signal say, “Hey, you look a lot like me.”

If you’re a student wondering what separates hand-wavy intuition from real-world results in signal processing, data science, or machine learning, this article is your invitation to take the inner product seriously—and see how it shows up almost everywhere.

👋 What Is the Inner Product?

At its most basic, the inner product is a measure of similarity between two vectors. In Euclidean space, it looks like this: $\langle \mathbf{a}, \mathbf{b} \rangle = \sum_{i=1}^{n} a_i b_i = \mathbf{a}^T \mathbf{b}$

If the vectors point in similar directions, their inner product is large and positive. If they’re orthogonal (perpendicular), it’s zero. If they point in opposite directions, it’s negative.

But here’s the kicker: the inner product isn’t just about geometry. It’s a universal tool for comparing any kinds of data—sounds, images, documents, signals, even entire distributions—so long as they can be represented as vectors. It’s math’s way of asking: “Do these two things line up?”

🎧 Signal Processing: The Original Playground

In signal processing, inner products are everywhere. Take the Fourier Transform. It decomposes a signal into sine and cosine waves. And it does this by computing the inner product of your signal $x(t)$ with basis functions like $\cos(2\pi ft)$ : $X(f) = \int x(t) \cdot e^{-2\pi i f t} dt$

That’s just a complex inner product! It’s asking: “How much does your signal resemble a sinusoid at frequency fff?” The answer—Fourier coefficients—becomes your signal’s frequency fingerprint.

This idea powers:

MP3 compression
Noise-canceling headphones
Sonar and radar detection
Voice assistants recognizing you

It’s also why two musical notes sound different: their frequency content—measured using inner products—isn’t the same.

🤖 Machine Learning: Similarity Is Everything

In machine learning, inner products show up in ways you’ve probably already seen, even if you didn’t notice:

Cosine similarity: Common in document search and recommendation systems. It’s just the normalized inner product: 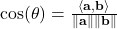$\cos(\theta) = \frac{\langle \mathbf{a}, \mathbf{b} \rangle}{\|\mathbf{a}\|\|\mathbf{b}\|}$ . So if your Netflix watch history aligns with someone else’s, this similarity measure helps recommend the same movies.
Linear classifiers: Models like logistic regression and support vector machines use the inner product to compute decision boundaries: 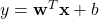$y = \mathbf{w}^T \mathbf{x} + b$ The result determines on which side of a hyperplane a point lies. The model is literally checking: “How aligned is your input with this learned direction?”
Neural networks: Each neuron computes an inner product between inputs and weights, then applies a nonlinearity. It’s a glorified dot product with a twist.

Even attention mechanisms in transformers—the backbone of large language models—use inner products between query and key vectors to determine which tokens should “pay attention” to each other.

🎮 Beyond Engineering: Where Else It Shows Up

You don’t need to be an engineer to see inner products in action:

Natural language processing (NLP): Word embeddings like Word2Vec or BERT rely on inner products to compare meanings. If “king – man + woman” ≈ “queen”, that’s because their vector representations align that way.
Psychology and neuroscience: Brain signals (like EEG or fMRI) are often decomposed into known patterns (basis functions) using inner products.
Art & image style transfer: Matching brushstroke “styles” involves computing correlations between feature maps—again, just inner products in high dimensions.
Finance: Portfolio risk modeling, asset correlation, and time series comparisons use covariance matrices—big grids of inner products.

Even quantum mechanics leans hard on inner products: the probability of finding a system in a given state is the magnitude squared of an inner product between state vectors.

🧠 Why Students Should Care

Inner products are not just theoretical tools—they’re practical, fast, and foundational. They’re the first step in almost every deeper technique you’ll learn.

Want to:

Build a speech recognizer? You’ll need to project audio onto basis functions (inner products).
Understand principal component analysis (PCA)? That’s eigenvectors of a covariance matrix—a matrix full of inner products.
Write better AI models? Learn when your inputs are aligned with the right directions in your feature space.

And unlike deep math theorems, inner products are visual and geometric. They make data tangible.

📏 Inner Products in New Forms

The beauty of the inner product is that it can be generalized. In fancier settings, it’s not just a dot product. It’s a function: $\langle \mathbf{a}, \mathbf{b} \rangle_G = \mathbf{a}^T G \mathbf{b}$

Where GGG is a positive definite matrix that redefines what similarity means. This is how kernel methods work in machine learning: they implicitly compute inner products in high-dimensional spaces using clever functions—like the radial basis function (RBF) kernel.

So inner products don’t just tell us whether two things are similar—they let us define how similarity should be measured.

Final Thought: The Hidden Glue of Modern Technology

Think of the inner product as the heartbeat of modern computation. It’s simple but profound. From detecting cancerous cells to guiding missiles, from recommending books to filtering your photos, it’s how we compare, filter, compress, and decide.

So, if you’re a student on the fence about whether that linear algebra class is worth your energy—remember this: mastering the inner product isn’t just about passing an exam. It’s about seeing the world through a clearer, more computational lens. And in the age of AI and data, that might just be your most valuable view.

Inner Product Linear Algebra Pattern Matching Signal Processing

The Inner Product: The Most Important Math You’re Already Using Without Realizing It