Listening to the Plate: How Lamb Waves Quietly Reveal the Structure of Materials

Disclaimer: this is an AI-generated article intended to highlight interesting concepts / methods / tools used within the SmartDATA Lab's research. This is for educating lab members as well as general readers interested in the lab. The article may contain errors.

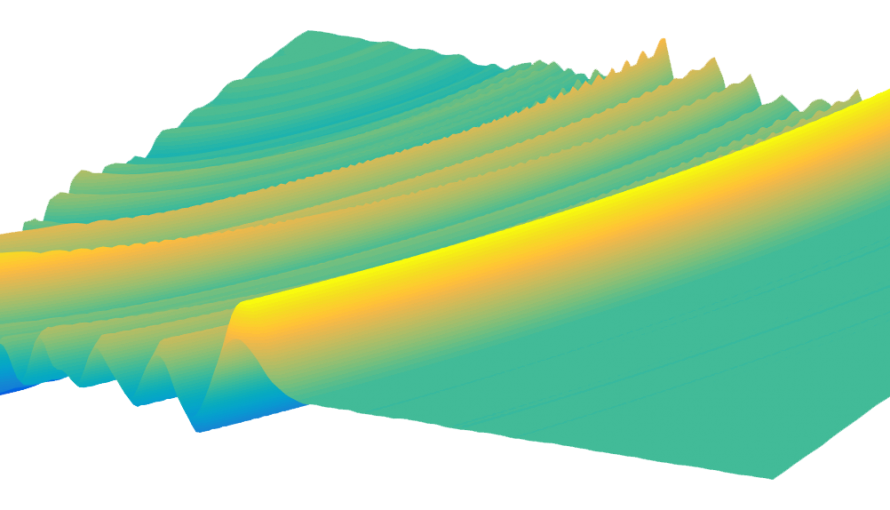
Guided waves like Lamb modes are reshaping how we inspect, model, and understand solid materials — all by listening to vibrations within the structure itself.

If you’ve never heard of Lamb waves, you’re not alone. Though they’ve been known to physicists and engineers for over a century, they remain surprisingly underdiscussed outside specialized fields like non-destructive testing, ultrasonics, and solid mechanics. But behind the scenes, Lamb waves are playing a crucial role — helping us understand how materials behave, age, and break, all through the language of wave motion.

They’re a fascinating mix of physics, engineering, and linear algebra — and they deserve more attention.

What Are Lamb Waves?

Lamb waves are a specific type of guided wave: mechanical vibrations that propagate through a thin solid plate, like a sheet of metal or glass. Unlike ordinary acoustic waves that travel through open air or infinite solids, Lamb waves are trapped between the top and bottom surfaces of a plate, making their behavior fundamentally different — and in many cases, more informative.

Named after the British mathematician Horace Lamb, who derived their governing equations in 1917, these waves are governed by the physics of elasticity and constrained geometry. They arise because the finite thickness of the material imposes boundary conditions — meaning the wave must behave in a way that “fits” the plate’s structure. This leads to complex patterns of motion involving both longitudinal (compressional) and transverse (shear) components.

Guided Doesn’t Mean Simple

One reason Lamb waves are so interesting is that they come in discrete modes, each with its own behavior. The most commonly discussed are the symmetric (S) and antisymmetric (A) modes:

Symmetric modes (S0, S1, …): The upper and lower surfaces of the plate move in sync.
Antisymmetric modes (A0, A1, …): The surfaces move in opposite directions, producing a sort of flexing motion.

At low frequencies, the A0 mode behaves like a flexural wave, while the S0 mode propagates more quickly and rigidly. These differences are not just academic — they’re used in practice to select the right wave for the right kind of material inspection or monitoring task.

Lamb waves are also dispersive, meaning that different frequencies travel at different speeds. This makes their analysis more complex, but also more powerful: by looking at how different components of a wave packet behave, you can extract fine details about the material it’s traveling through.

The Mathematics Behind the Motion

Understanding Lamb waves involves solving the elastodynamic wave equation under boundary constraints. This leads to what is essentially a complex eigenvalue problem — a cornerstone of linear algebra.

Here’s a simplified version of what’s happening mathematically:

$\nabla \cdot \boldsymbol{\sigma} = \rho \frac{\partial^2 \mathbf{u}}{\partial t^2}$

where:

$\boldsymbol{\sigma}$ is the stress tensor,
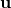$\mathbf{u}$ is the displacement field,
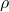$\rho$ is the material density.

By assuming a wave-like solution — say, a function like $\mathbf{u}(x,z,t) = \mathbf{U}(z) e^{i(kx - \omega t)}$ — the problem becomes a matter of finding solutions that satisfy the plate’s boundary conditions at its top and bottom surfaces.

This turns the partial differential equation into a transcendental equation involving wave speed, frequency, and material properties. Solutions to this equation describe the allowed modes, each of which is a kind of natural vibration pattern for the plate — similar to how a violin string vibrates at specific frequencies.

From a mathematical point of view, this is a rich problem: eigenmodes, dispersion relations, and mode coupling all play a role, and the geometry of the material (especially thickness) directly influences the solution space.

Practical Applications: Quiet Diagnostics

Lamb waves are particularly useful in non-destructive evaluation (NDE) — a field that aims to inspect the integrity of materials without damaging them. Because Lamb waves can travel long distances while remaining sensitive to tiny structural changes, they are ideal for monitoring things like:

Fatigue cracks in aircraft fuselages
Corrosion in buried pipelines
Delamination in composite materials
Structural changes in bridges or rail lines

Engineers can place sensors on the surface of a structure and send a Lamb wave down the material. By analyzing how the wave reflects or scatters — especially if certain modes are delayed or altered — they can infer internal damage, even when it’s invisible from the outside.

Why They’re Not More Widely Known

Despite their utility, Lamb waves haven’t entered the public scientific imagination the way, say, gravitational waves or quantum tunneling have. This may be because the mathematics involved is less often taught at an introductory level, or because the physical intuition takes time to develop.

Lamb waves also don’t lend themselves to simple visualization: they involve coupled modes, dispersive behavior, and multiple directions of motion all at once. But for those willing to dig in, they offer a window into how geometry, material properties, and wave mechanics interact in surprisingly subtle ways.

Looking Ahead

As materials become thinner, more complex, and more engineered — from composites to nanostructures — the importance of understanding guided waves like Lamb modes is only growing. With modern sensing technologies and computational tools, we’re now able to explore these waves in real time, and even design systems that actively shape or tune the wave behavior for specific tasks.

Whether you’re building aircraft, inspecting infrastructure, or modeling biological tissues, Lamb waves offer a powerful, precise, and often underappreciated tool.

Final Thought

Lamb waves sit at a fascinating intersection of applied math, physics, and engineering. They remind us that materials are not silent — they respond, resonate, and reveal their inner workings if we know how to listen.

Understanding these waves doesn’t require mysticism or advanced degrees — just a bit of curiosity, and maybe a willingness to look at a matrix or two.

📚 Relevant Lab Publications

1. Data-Driven Matched Field Processing for Lamb Wave Structural Health Monitoring

Authors: Joel B. Harley, José M. F. Moura
Publication: The Journal of the Acoustical Society of America, 135(3), 1231–1244 (2014)
Summary: This paper introduces a data-driven matched field processing approach for localizing structural damage using Lamb waves. The method leverages measured wavefields to create models that can detect and locate anomalies without requiring detailed knowledge of the structure’s material properties.ResearchGate+1Google Scholar+1 Google Scholar+1Google Scholar+1 SmartDATA Lab+3ResearchGate+3Google Scholar+3

2. Sparse Recovery of the Multimodal and Dispersive Characteristics of Lamb Waves

Authors: Joel B. Harley, José M. F. Moura
Publication: The Journal of the Acoustical Society of America, 133(5), 2732–2745 (2013)
Summary: This study presents a sparse wavenumber analysis technique to recover the multimodal and dispersive properties of Lamb waves from limited measurements. The approach addresses the challenges posed by the complex nature of guided wave propagation in plates.ResearchGate+3ResearchGate+3PubMed+3

3. Statistical Partial Wavefield Imaging Using Lamb Wave Signals

Author: Joel B. Harley
Publication: Structural Health Monitoring, 17(6), 1386–1397 (2018)
Summary: The paper proposes a statistical imaging method that utilizes partial Lamb wavefield measurements to detect and visualize structural damage. The technique offers a baseline-free approach, enhancing practicality in real-world applications. SmartDATA Lab+1SAGE Journals+1

4. Learning Guided Wave Dispersion Curves from Multi-Path Reflections with Compressive Sensing

Authors: Joel B. Harley, K. Supreet Alguri, Harsha Vardhan Tetali, Soroosh Sabeti
Conference: Structural Health Monitoring 2019
Summary: This research employs compressive sensing to learn dispersion curves of guided waves from multi-path reflections. The method improves the efficiency of characterizing wave propagation in complex structures with fewer measurements.codeocean.com+3ResearchGate+3ResearchGate+3 codeocean.com+3Wikipedia+3ResearchGate+3

📚 Want to Learn More? Here Are Some Excellent Academic Sources:

Rose, J. L. (2014). Ultrasonic Guided Waves in Solid Media. Cambridge University Press.
– A comprehensive resource on guided waves, including Lamb wave theory and applications.
Viktorov, I. A. (1967). Rayleigh and Lamb Waves: Physical Theory and Applications. Plenum Press.
– A classic and foundational text on surface and plate wave mechanics.
Giurgiutiu, V. (2008). Structural Health Monitoring with Piezoelectric Wafer Active Sensors. Academic Press.
– Discusses practical implementation of Lamb wave sensors in structural monitoring systems.
Alleyne, D. N., & Cawley, P. (1992). “The Interaction of Lamb Waves with Defects.” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 39(3), 381–397.
– A highly cited paper on Lamb waves and their use in detecting defects.
Lowe, M. J. S. (1995). “Matrix Techniques for Modeling Ultrasonic Waves in Multilayered Media.” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 42(4), 525–542.
– Offers an elegant matrix-based approach to modeling Lamb wave propagation, especially relevant to layered structures

Eigenmodes Lamb Wave Linear Algebra Materials Mechanics Nondestructive Testing Structural Health Monitoring

Listening to the Plate: How Lamb Waves Quietly Reveal the Structure of Materials