Code and Resources
This page provides freely available code and notes for other researchers to use and share. All of our code is published on CodeOcean, which allows anyone to interact with the code without needing to download it. All of the codes are versioned, preserved, and run on their original coding platform in CodeOcean.
Table of Contents
Sparse Wavenumber Analysis
Interactive code: https://doi.org/10.24433/CO.2630229.v1
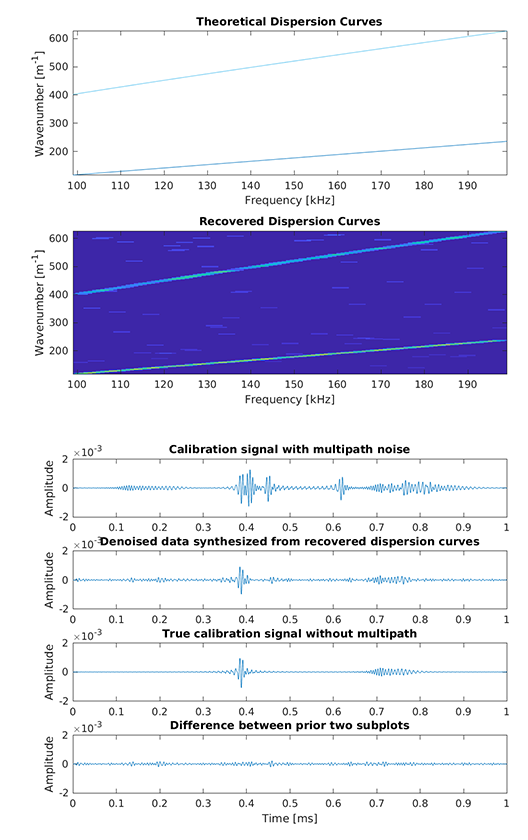
In this script, we show an example of applying sparse wavenumber analysis (SWA) to simulation data corrupted by multipath interference. This learns the dispersion curves (i.e., the frequency-wavenumber representation) of wave data.
The variable ‘xm’ contains the multipath “measured” simulation data. The multipath data is used as the input to sparse wavenumber analysis (SWA).
The variable ‘xc’ contains the ideal (no multipath) simulation data. This data is used to evaluate our sparse wavenumber denoising results — i.e., test if the denoised data matches the true ideal data.
The variable ‘xp’ contains a set of ideal responses from random locations (not used in the training) in the medium. This data is used to evaluate our sparse wavenumber prediction results — i.e., can we accurately predict other “measured” signals from the medium.
The script uses two particular functions: SWA and SWS.
SWA performs sparse wavenumber analysis on the data ‘xm’ at frequency samples ‘fn’ and over a wavenumber domain ‘k’. Sparse wavenumber analysis can be performed using one of two methods currently: basis pursuit denoising (‘bp’) or orthogonal matching pursuit (‘omp’). The variables ‘Rxc’ and ‘Txm’ represent the locations of the receivers and transmitters for sparse wavenumber analysis, respectively. The variable ‘Rxp’ represents the locations of the receivers for prediction. The variable ‘tau’ represents the number of sparse components for orthogonal matching pursuit. The output ‘V’ of sparse wavenumber analysis is a matrix of the data’s frequency-wavenumber representation.
SWS performs sparse wavenumber synthesis given a frequency-wavenumber representation ‘V’ over a wavenumber domain ‘k’. The variables ‘Rxm’ and ‘Txm’ or ‘Rxp’ and ‘Txp’ represent the locations for transmitters and receivers.
Data-Driven Matched Field Processing
Interactive code: https://doi.org/10.24433/CO.0906211.v1
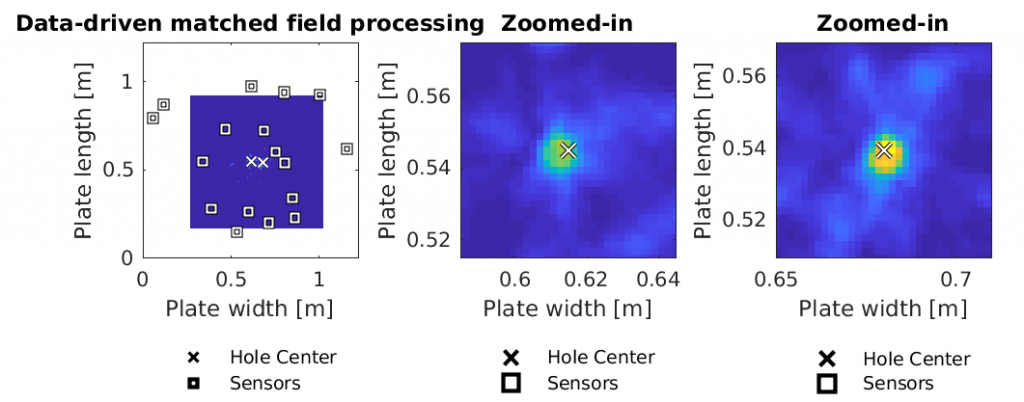
This code introduces data-driven matched field processing, a framework to build models of multimodal propagation environments from measured data and then uses these models to locate damage. The example code demonstrates data-driven matched field processing’s localization performance with two nearby scatterers from experimental measurements on an aluminum plate. When compared with delay-based models that are commonly used in structural health monitoring, data-driven matched field processing successfully localizes both scatterers with significantly smaller localization errors and finer resolutions.
Temporal Sparse Wavenumber Analysis
Interactive code: https://doi.org/10.24433/CO.1017684.v1
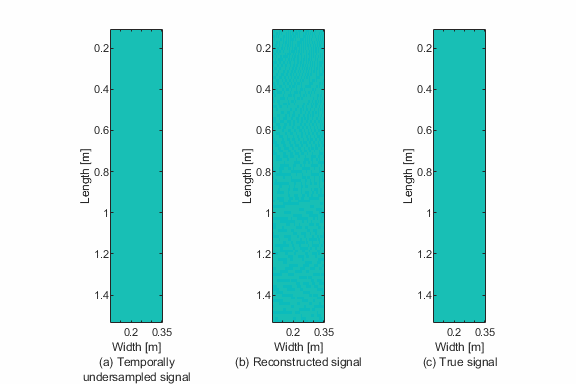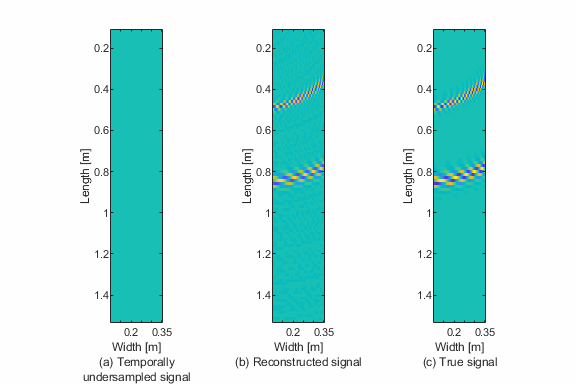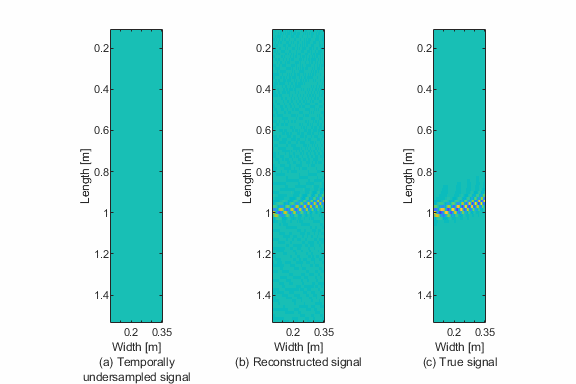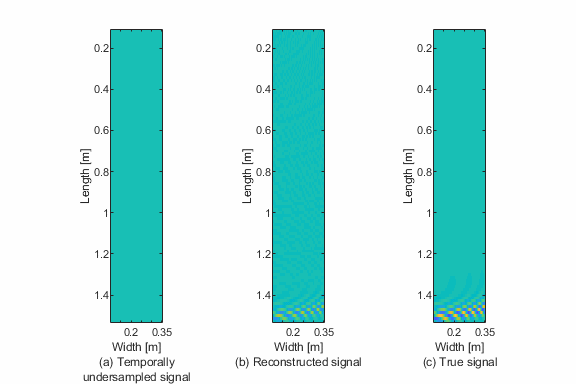
This script demonstrates temporal sparse wavenumber analysis to reconstruct / complete guided wave / Lamb wave data from temporally incomplete measurements. This is demonstrated with simulated Lamb wave data.
K-SVD / Dictionary Learning for Guided Wave Damage Detection
Interactive code: https://doi.org/10.24433/CO.2764739.v1
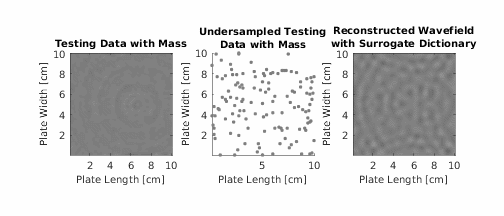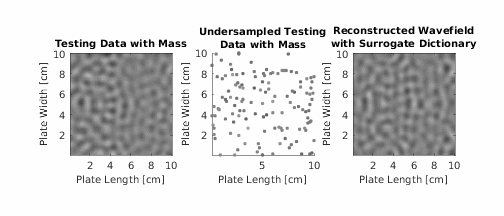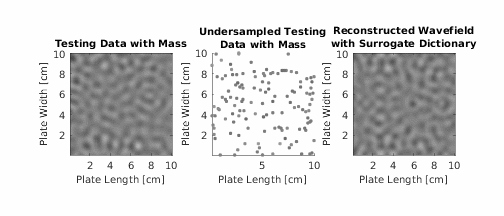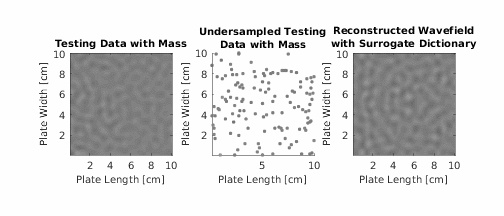
In guided wave structural health monitoring, damage detection is often accomplished by comparing measurements before damage (i.e., baseline data) and after damage (i.e., test data). Yet, in practical scenarios, baseline data is often unavailable. Data from surrogate structures (structures similar to the test structure) could replace baseline data, but due to small differences in material properties, such as thickness, temperature, and other effects, this data is often unreliable. In this paper, a dictionary learning framework overcomes this challenge and detects damage with surrogate information. The framework combines wave propagation characteristics of a test structure with geometric information from surrogate structures to create a synthetic damage-free baseline. The test data is compared with the synthetic baseline to detect damage. The framework is evaluated with 108 mm ×108 mm steel and aluminum plates. The framework is applied to each test structure after learning from plates with different material properties and thicknesses. With full wavefield data, this paper successfully isolates reflections from a mass without using explicit baseline data. Furthermore, with sparse guided wave data, this paper shows that a drop in a correlation coefficient can detect a mass without using explicit baseline data.
Dynamic Time Warping Temperature Compensation for Guided Wave Structural Health Monitoring
Interactive code: https://doi.org/10.24433/CO.0678166.v1
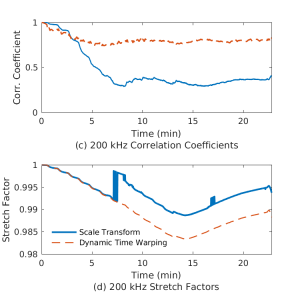
Guided wave structural health monitoring is widely researched for remotely inspecting large structural areas. To detect, locate, and characterize damage, guided wave methods often compare data to a baseline signal. Yet, environmental variations create large differences between the baseline and the collected measurements. These variations hide damage signatures and cause false detection. Temperature compensation algorithms, such as baseline signal stretch and the scale transform have been used to optimally realign data to a baseline. While these methods are effective in some conditions, their performance deteriorates in the presence of large temperature variations, long propagation distances, and high frequencies. In this code, we use dynamic time warping to better align guided wave data and to overcome these errors. When compared with stretch-based methods, we show that the dynamic time warping is more robust to the above-mentioned errors and more accurately detects damage with weak ultrasonic signatures.
Statistical Partial Wavefield Imaging
Interactive code: https://doi.org/10.24433/CO.3027030.v1
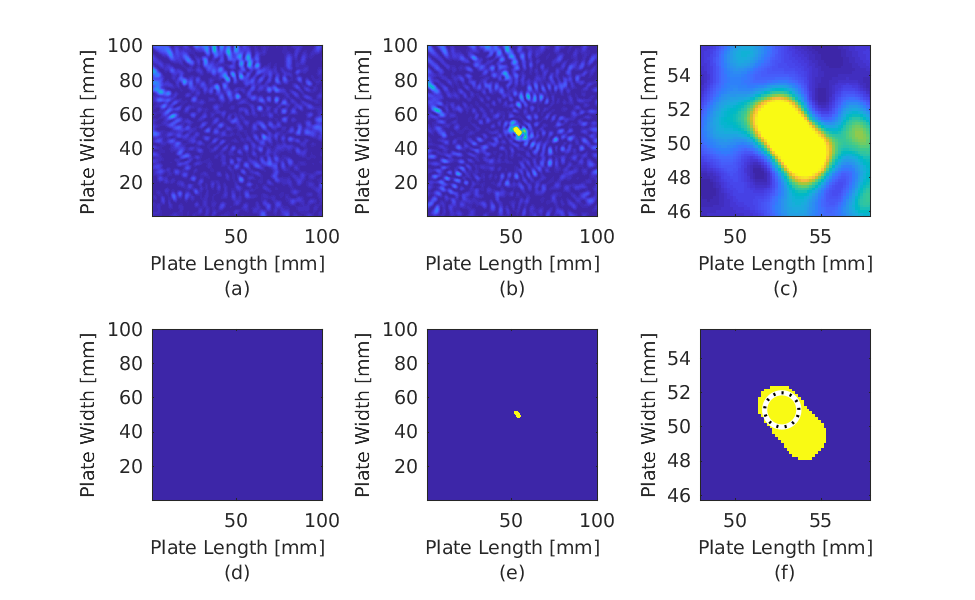
This code presents a baseline-free, model-driven, statistical damage detection and imaging framework for guided waves measured from partial (i.e. non-dense) wavefield scans. Wavefield analysis is an effective non-contact technique for non-destructive evaluation. Yet, there are several limitations to practically implement wavefield methods. These limitations include slow data acquisition and a lack of statistical reliability. Our approach addresses both of these challenges. We use sparse wavenumber analysis, sparse wavenumber synthesis, and data-fitting optimization to accurately model damage-free wavefield data. We then combine this model with matched field processing to image damage from a small number of partial wavefield measurements. We further derive a hypothesis test based on extreme value theory to statistically detect damage. We test our framework with Lamb wave measurements from a steel plate. With 70 experimental wavefield measurements, we achieve an empirical probability of damage detection of more than 98%, an empirical probability of false alarm of less than 0.17%, and an accurate image of the damage.
Transmission Line Simulation with an Algebraic Graphical Model
Interactive code: https://doi.org/10.24433/CO.8214677.v1
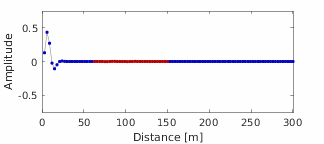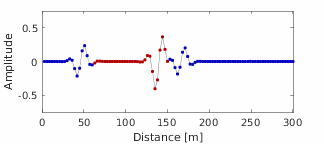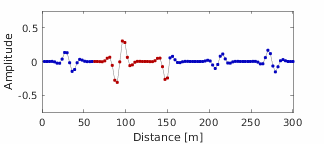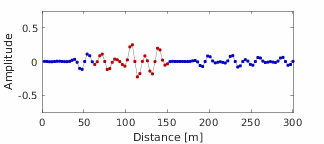
This code demonstrates a computationally efficient algebraic graph theory engine for simulating time-domain one-dimensional waves in a multi-segment transmission line, such as for reflectometry applications. Efficient simulation of time-domain signals in multi-segment transmission lines is challenging because the number of propagation paths (and therefore the number of operations) increases exponentially with each new interface. We address this challenge through the use of a frequency-domain, algebraic graphical model of wave propagation, which is then converted to the time domain via the Fourier transform. We use this model to achieve an exact, stable, and computationally efficient [O(NQ), where N is the number of segments and Q is the bandwidth] approach for studying one-dimensional wave propagation. Our approach requires the reflection and transmission coefficients for each interface and each segment’s complex propagation constant. We compare our simulation results with known analytical solutions.
Sparse Wavenumber Recovery and Prediction of Anisotropic Guided Waves in Composites: A Comparative
Interactive code: https://doi.org/10.1109/tuffc.2019.2918746
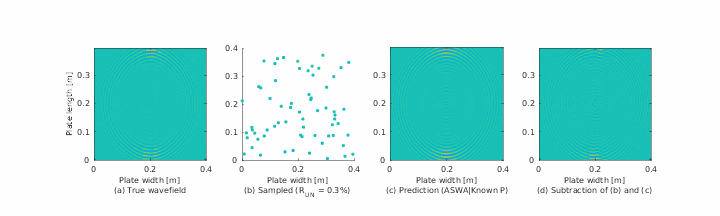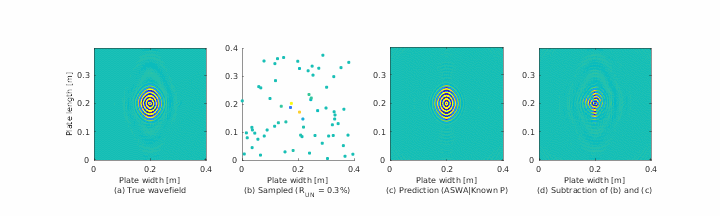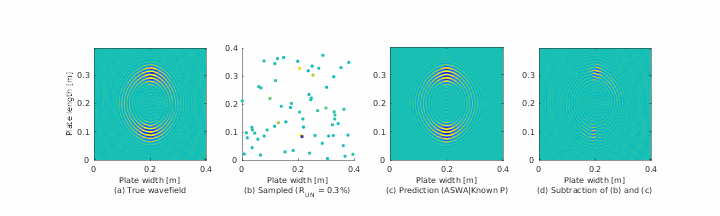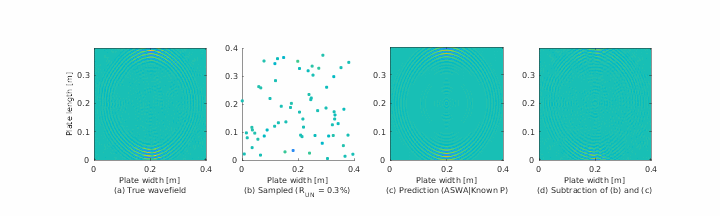
Guided wave methodologies are among the established approaches for structural health monitoring (SHM). For guided wave data, being able to accurately estimate wave properties in the absence of ample measurements can greatly facilitate the often time-consuming and potentially expensive data acquisition procedure. Nevertheless, inherent complexities of the guided waves, including their multimodal and frequency dispersive nature, hinder processing, analysis, and behavior prediction. The severity of these complexities is even higher in anisotropic media, such as composites. Several methods, including sparse wavenumber analysis (SWA), have been proposed in the literature to characterize guided wave propagation by extracting wave characteristics in a particular medium from the information contained in a few measurements, and subsequently using this information for full wavefield prediction. In this paper, we investigate the efficacy of guided wave reconstruction techniques, based on SWA, for predicting the behavior of guided waves in composite materials. We implement these techniques on several experimental and simulation data sets. We study their performance in estimating the frequency-dependent (dispersive) and anisotropic velocities of guided waves and in reconstructing full wavefields from limited available information.
Spread Spectrum Time Domain Reflectometry with Lumped Elements on Asymmetric Transmission Lines
Interactive code: https://doi.org/10.24433/CO.5338695.v1
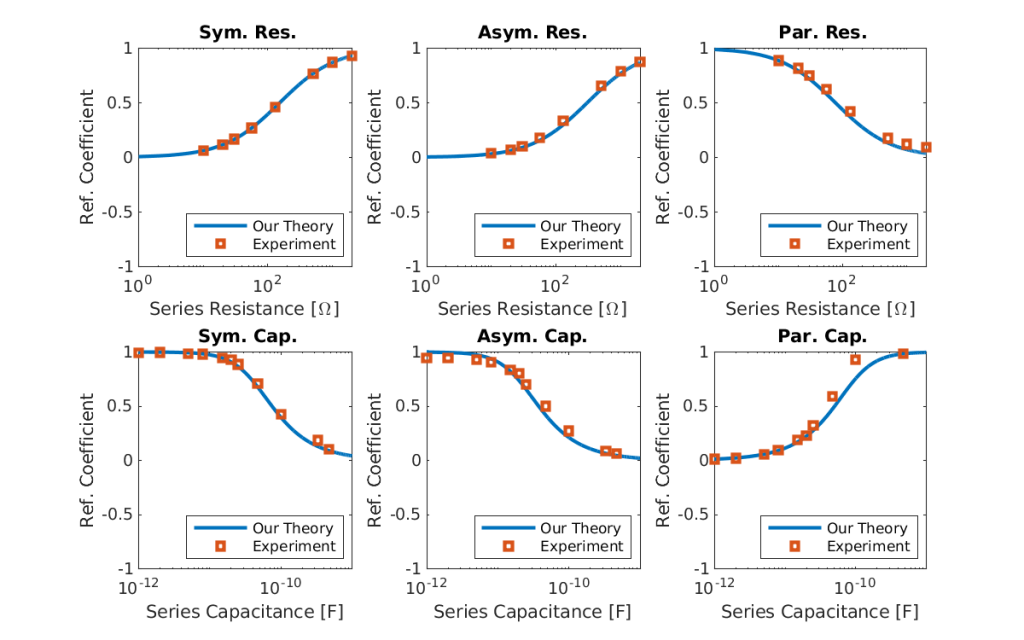
Spread spectrum time domain reflectometry (SSTDR) has been traditionally used to detect hard faults (open and short circuit faults) in transmission lines. Prior work has focused on loads at the end of the line with little research on impedances from circuit elements located in the middle of the line (i.e., not at the load) or on only one wire of the line. In this work we consider cases of transmission lines with different impedances on each wire. We refer to lines with the same impedance on both wires (positive and negative) as symmetric. Lines with different impedances on each wire are asymmetric. For highly localized impedances (approximately infinitesimal in length, i.e. with a length significantly smaller than the wavelength of the incident signal), the reflections and their effects on the propagating wave become difficult to describe with traditional transmission line theory. We provide analytical expressions for reflection coefficients for symmetric and asymmetric transmission lines and show that these formulae describe experimental measurements of capacitors and resistors to about 99% accuracy for the magnitudes and 75% for the phases.

