Sparse Wavenumber Recovery in Anisotropic Composites Repository

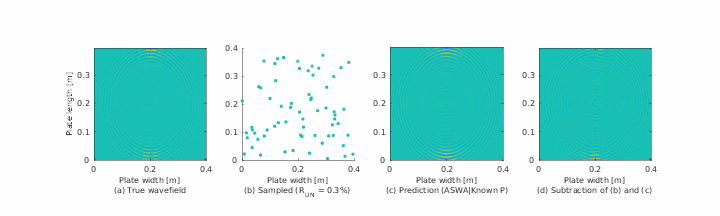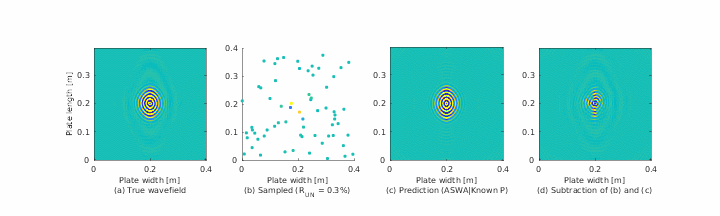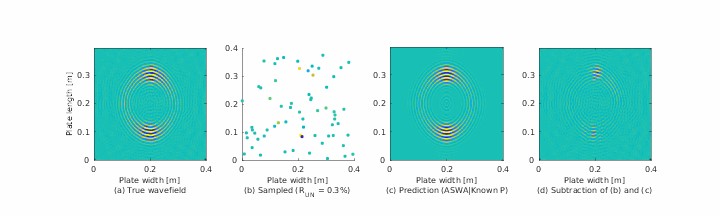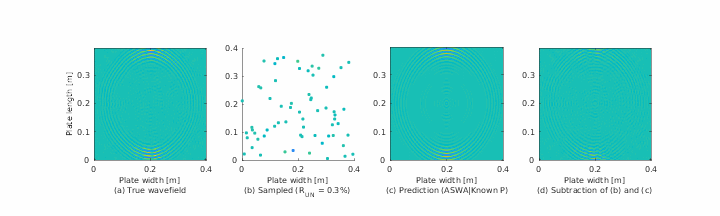
Joel B. Harley July 15, 2025 Code & Resources 0

Summary

Guided wave imaging is a cornerstone technique in structural health monitoring (SHM), especially for composite materials. But composites are anisotropic—meaning wave speeds and behaviors vary with direction—which makes interpreting wave propagation challenging.

This CodeOcean capsule presents the algorithm and tools for Sparse Wavenumber Recovery (SWR) developed by Soroosh Sabeti, which leverage compressed sensing and sparse signal processing to efficiently extract anisotropic wavenumber content from limited measurements.

🎯 Why This Matters

Conventional Fourier-based methods for wavefield analysis (e.g., 2D FFT) require dense spatial sampling, which is impractical in many real-world settings. SWR addresses this limitation by enabling:

Accurate recovery of direction-dependent wavenumbers (i.e., dispersion),
From sparse or non-uniform measurements,
While remaining robust to anisotropic material behaviors, such as in carbon fiber composites.

📐 Core Technical Idea

Given a spatial wavefield snapshot $u(x, y, t)$ , the goal is to identify the dominant wavenumber vectors $\vec{k}$ that represent wave propagation at different angles $\theta$ .

Traditional methods use the 2D spatial Fourier transform: $\hat{u}(k_x, k_y) = \mathcal{F}$

but require Nyquist-level sampling. Instead, Sparse Wavenumber Recovery solves:

$\min_{\alpha} \| \alpha \|_1 \quad \text{subject to} \quad u = \Phi \Psi \alpha$

where:

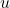$u$ : measured spatial wavefield vector (possibly under-sampled),
$\Phi$ : sampling matrix,
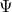$\Psi$ : wavenumber dictionary (e.g., plane wave atoms at various $\vec{k}$ ),
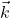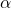$\alpha$ : sparse representation of wavefield in the wavenumber domain.

This formulation promotes sparse solutions—capturing only the most physically meaningful wave directions and speeds.

🧪 What’s in the Repository?

The CodeOcean capsule includes:

✅ MATLAB scripts to implement sparse recovery using L1-norm minimization,
📊 Visualizations of anisotropic wave propagation in composite panels,
🧠 Comparative studies with traditional FFT and MUSIC algorithms,
📂 Sample data from finite element simulations and experiments.

🔬 What Did the Paper Show?

The authors tested SWR on both simulated and experimental Lamb wave data from composite plates. Their results show:

SWR accurately reconstructs anisotropic dispersion curves, even from 10–20% of spatial data.
It outperforms MUSIC and FFT in both angular resolution and robustness to noise.
The method reveals direction-dependent wave speeds and mode interactions not easily seen in conventional spectra.

💡 Real-World Impact

🛩️ Ideal for aerospace composites and curved laminate structures,
🔎 Supports SHM systems with limited sensor counts,
🧱 Can be combined with machine learning for automated defect detection,
📉 Enables better modal separation and phase velocity estimation.

📚 Reference

Sabeti, S., Leckey, C. A. C., De Marchi, L., & Harley, J. B. (2019).
Sparse Wavenumber Recovery and Prediction of Anisotropic Guided Waves in Composites: A Comparative Study.
IEEE Trans. on Ultrasonics, Ferroelectrics, and Frequency Control, 66(8), 1352–1363.
🔗 https://ieeexplore.ieee.org/document/8721165

This repository offers a practical, efficient, and research-validated toolkit for guided wave analysis in complex composite structures. Whether you’re designing SHM systems, interpreting wavefields, or experimenting with anisotropy-aware imaging, SWR gives you sharper insights with fewer sensors.

Sparse data. Rich understanding.

Anisotropy Eigenmodes Lamb waves Linear Algebra Mechanics Nondestructive Testing Sparse Wavenumber Analysis Structural Health Monitoring Undersampling

Sparse Wavenumber Recovery in Anisotropic Composites Repository