K-SVD Dictionary Learning for Damage Detection Repository

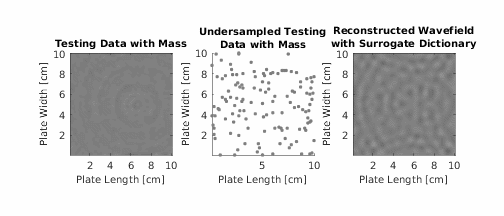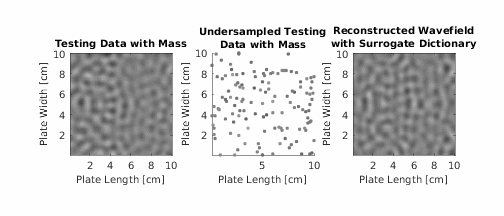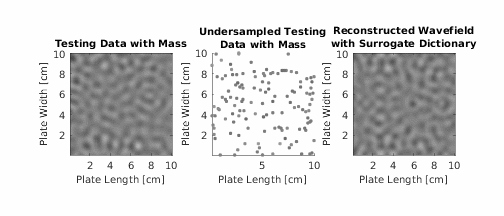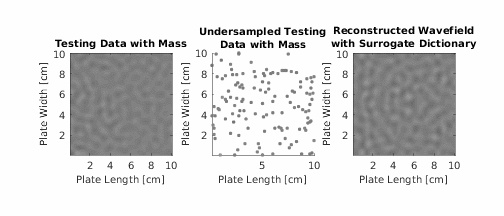
Joel B. Harley June 10, 2025 Code & Resources 0

Summary

K-SVD Dictionary Learning for Damage Detection is a baseline-free, data-driven approach for detecting structural damage using guided ultrasonic waves. Developed by Supreet Alguri and Dr. Joel B. Harley, this method eliminates the need for pristine baseline measurements—a major limitation in many real-world Structural Health Monitoring (SHM) systems.

This CodeOcean capsule provides a reproducible implementation of the algorithm, as described in the paper:

Alguri, K. S., Melville, J., & Harley, J. B. (2018). Baseline-free guided wave damage detection with surrogate data and dictionary learning. The Journal of the Acoustical Society of America, 143(6), 3320–3331. https://doi.org/10.1121/1.5042753

🧩 The Challenge: Baseline-Free Damage Detection

Most guided wave damage detection methods rely on baseline signals—measurements from an undamaged structure. But in real-world environments, obtaining such baselines is often impractical or impossible due to:

Aging infrastructure
Limited access to pristine states
Environmental variability over time

This algorithm solves that problem by learning the characteristics of undamaged behavior directly from current (possibly damaged) data—no prior baseline required.

🧠 The Solution: Dictionary Learning via K-SVD

The method uses the K-SVD algorithm to learn a dictionary of atoms (signal features) that represent the undamaged wavefield behavior. If a new signal cannot be well-represented by this learned dictionary, it’s likely that damage is present.

Step-by-step:

Collect signals from a sensor network on the structure.
Learn a dictionary using the K-SVD algorithm:
- Solve:
  - $Y$ : matrix of training signals
  - $X$ : sparse coefficients
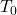  - $T_0$ : sparsity constraint
Compute reconstruction error for new measurements:
- For a new signal 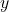$y$ , solve: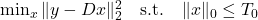 $\min_x \|y - Dx\|_2^2 \quad \text{s.t.} \quad \|x\|_0 \leq T_0$
- If the error 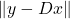$\|y - Dx\|$ exceeds a threshold, damage is detected.

📦 What’s Inside This Capsule?

✅ Full MATLAB implementation of K-SVD and sparse coding
🧪 Synthetic and experimental guided wave datasets
📊 Tools for computing reconstruction errors and generating detection maps
📘 Documentation and examples for ease of use

🏆 Why Use This Method?

🔍 No baseline required — Learn “healthy” behavior directly from operational data.
⚡ Robust to variability — Handles environmental and operational changes without false positives.
🧠 Data-driven — Uses machine learning to discover signal patterns without physical modeling.
🧰 Portable and scalable — Suitable for both small and large structures.

📚 Reference

Alguri, K. S., Melville, J., & Harley, J. B. (2018). Baseline-free guided wave damage detection with surrogate data and dictionary learning. The Journal of the Acoustical Society of America, 143(6), 3320–3331.
🔗 https://doi.org/10.1121/1.5042753

Eigenmodes Lamb Wave Linear Algebra Nondestructive Testing Sparse Wavenumber Analysis Structural Health Monitoring

K-SVD Dictionary Learning for Damage Detection Repository