Temporal Sparse Wavenumber Analysis Repository

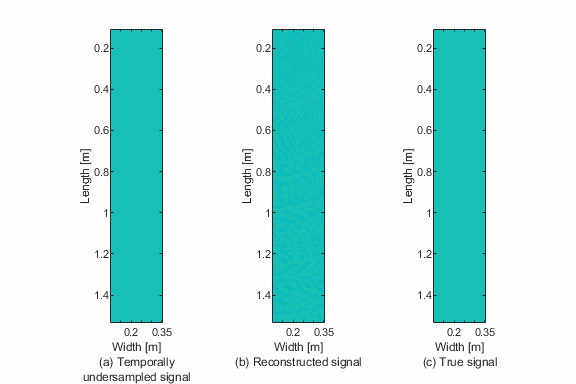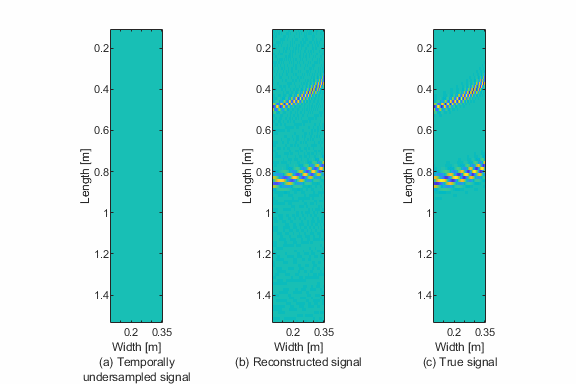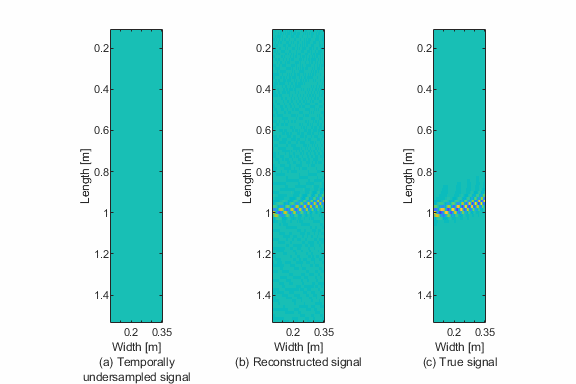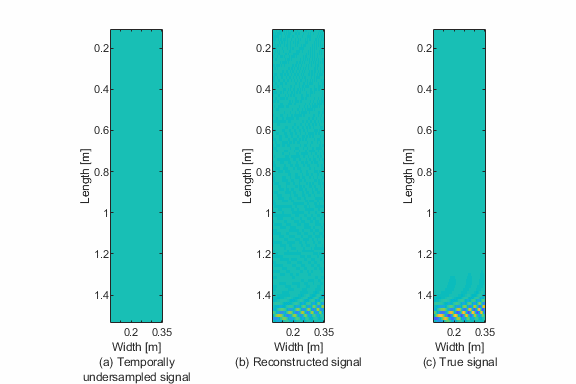
Joel B. Harley June 3, 2025 Code & Resources 0

Summary

Temporal Sparse Wavenumber Analysis (TSWA) is a novel technique that reconstructs high-resolution spatiotemporal wavefields using fewer temporal samples than traditional methods typically require. Developed by Soroosh Sabeti and Dr. Joel B. Harley, TSWA makes it possible to retrieve accurate guided wave information from temporally undersampled data, which is crucial in applications where high-speed sensing, data storage, or power consumption are limiting factors.

This CodeOcean capsule contains a full implementation of TSWA, as described in:

Sabeti, S., & Harley, J. B. (2017). Guided wave retrieval from temporally undersampled data. 2017 IEEE International Ultrasonics Symposium (IUS), 1–4. https://doi.org/10.1109/ULTSYM.2017.8091996

🌊 Why TSWA?

Conventional methods of wavefield reconstruction require Nyquist-rate temporal sampling, leading to high data acquisition and storage burdens. In practice, this restricts sensing systems on resource-constrained platforms like embedded SHM systems or UAVs. TSWA overcomes this by using compressive sensing to reconstruct wavefields from fewer temporal samples, enabling efficient, high-resolution guided wave analysis without compromising signal integrity.

🧠 How It Works

The core idea of TSWA is to exploit the sparsity of a wavefield in the wavenumber domain and recover full-resolution temporal signals from sub-sampled data using sparse optimization.

Let:

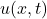$u(x, t)$ be the recorded wavefield at spatial location 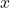$x$ and time $t$ .
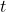The wavefield is modeled as a superposition of a sparse set of propagating plane waves.

TSWA assumes that the wavefield can be expressed as:

$u(x, t) \approx \sum_{n=1}^N a_n e^{j(k_n x - \omega_n t)}$

Where:

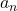$a_n$ are the complex amplitudes,
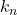$k_n$ are candidate spatial frequencies (wavenumbers),
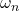$\omega_n$ are the associated angular frequencies.

If we denote the temporally undersampled measurement vector as $\mathbf{y}$ , the reconstruction problem becomes: $\min_{\mathbf{a}} \|\mathbf{y} - \Phi \mathbf{a} \|_2^2 + \lambda \|\mathbf{a}\|_1$

Where:

$\Phi$ is the dictionary matrix of plane waves evaluated at known spatial and undersampled temporal locations,
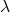$\lambda$ is a regularization parameter enforcing sparsity.

This sparse recovery allows reconstruction of the full spatiotemporal wavefield, even from temporally incomplete data.

⚙️ What’s in This Capsule?

✅ Full MATLAB implementation of the TSWA algorithm
📂 Synthetic and experimental datasets for demonstration
📊 Tools to visualize reconstructed wavefields and compare with ground truth
📘 Documentation and usage examples for reproducibility

🏆 Key Benefits

🕒 Reduced temporal sampling — up to 50% fewer time points with minimal loss in accuracy
🎯 High-resolution wavefield reconstruction — sharp, artifact-free spatiotemporal profiles
⚡ Efficiency — lowers data acquisition and processing demands
🧱 Adaptable — compatible with structural health monitoring, NDE, and ultrasonics

📚 Reference

Sabeti, S., & Harley, J. B. (2017). Guided wave retrieval from temporally undersampled data. In 2017 IEEE International Ultrasonics Symposium (IUS) (pp. 1–4). IEEE. https://doi.org/10.1109/ULTSYM.2017.8091996

Eigenmodes Lamb Wave Linear Algebra Nondestructive Testing Sparse Wavenumber Analysis Structural Health Monitoring Undersampling

Temporal Sparse Wavenumber Analysis Repository